こんにちは！営業部の加藤です。
このブログには初登場になります。
元某パチンコ系雑誌の編集者として、面白い記事を
提供しようと思いますので、よろしくお願い致します！

さて、記念すべきブログの初回テーマは・・・
「モンティ・ホール問題」にしたいと思います。
ちなみにコレは環境問題とか人権問題ではありません（＾＾；
モンティ・ホール問題とは、確率論の問題ではよく出てくる題材で、
非常に面白いと思うので、ここで紹介したいと思います。

まずはちょっとした画像を作ってみましたので、
画像を気軽にポチって下さい。
（変な広告は出ませんのでご安心を・・・）

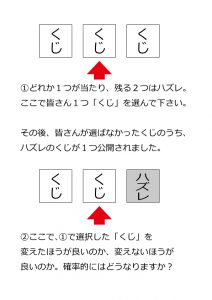
①・３つの中で１つ当たりと思うくじを選ぶ。（当たりは１つ）
②・選ばれなかったくじのうち、「ハズレ」を公開。
③・この時「①」で選んだくじを変えたほうが良いか、
変えないほうが良いか答えなさい。

・・・という問題です。

まず①の状況では３つのくじのうち、当たりが１つなので
確率的には当然1/3になります。これはOKですね。
では・・・その後でハズレが一枚公開された時点ではどうでしょうか。
1/2？1/3？いくつでしょうか。最初から1/3のまま？
くじは変えなくても同じ？？？

 

１行だけ間をあけますので、ちょっと考えてみて下さい。

 

では答え・・・いきます！

③の時点で選んだくじを変えたほうが確率的には良い。です。
確率的には①の時点で1/3ですが、③の時点で選んだくじを変える事により、
当たる確率は2/3になるからです！ど～ん！

もしこれが最初から理解できていたら、
あなたは世界最高のIQをもっているかも（＾＾）
え？どうして？なぜ？おかしい！という人は、
ぜひ「モンティ・ホール問題」で検索してみて下さい。
（クリックして飛ぶようにしておきました）

 

パチンコやパチスロ、公営ギャンブル、麻雀、ポーカー
ルーレットなど、世の中の賭け事には全て確率論が関わります。
常勝は無理でも勝率51%以上を目指す人は、
ぜひ基本となる確率論という武器を身に着けておくと良いと思いますよ。

ここはあまり書くと長文になるので、
今日はこの辺でお暇します（＾＾）

 

では皆様！また次回お愛しましょう～ノシ